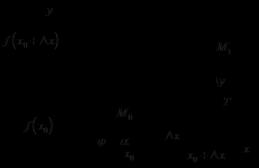Непрерывность функции имеющей производную дифференциал. Производная

Задача о скорости движущейся точки

Пусть – закон прямолинейного движения материальной точки. Обозначим через путь, пройденный точкой за время , а через путь, пройденный за время . Тогда за время точка пройдет путь , равный: . Отношение называется средней скоростью точки за время от до . Чем меньше , т.е. чем короче промежуток времени от до , тем лучше средняя скорость характеризует движение точки в момент времени . Поэтому естественно ввести понятие скорости в данный момент , определив ее как предел средней скорости за промежуток от до , когда :

Величина называется мгновенной скоростью точки в данный момент .

Задача о касательной к данной кривой

Пусть на плоскости задана непрерывная кривая уравнением . Требуется провести невертикальную касательную к данной кривой в точке . Так как точка касания дана, то для решения задачи требуется найти угловой коэффициент касательной. Из геометрии известно, что , где – угол наклона касательной к положительному направлению оси (см. рис.). Через точки и проведем секущую , где – угол, образованный секущей с положительным направлением оси . Из рисунка видно, что , где . Угловой коэффициент касательной к данной кривой в точке может быть найден на основании следующего определения.

Касательной к кривой в точке называется предельное положение секущей , когда точка стремится к точке . Отсюда следует, что .

Определение производной

Математическая операция, требуемая для решения рассмотренных выше задач, одна и та же. Выясним аналитическую сущность этой операции, отвлекаясь от вызвавших ее конкретных вопросов.

Пусть функция определена на некотором промежутке. Возьмем значение из этого промежутка. Придадим какое-нибудь приращение (положительное или отрицательное). Этому новому значению аргумента соответствует и новое значение функции , где .

Составим отношение , оно является функцией от .

Производной функции по переменной в точке называется предел отношения приращения функции в этой точке к вызвавшему его приращению аргумента , когда произвольным образом:

Замечание. Считается, что производная функции в точке существует, если предел в правой части формулы существует и конечен и не зависит от того, как приращение переменной стремится к 0 (слева или справа).

Процесс нахождения производной функции называется ее дифференцированием.

Нахождение производных некоторых функций по определению

а) Производная постоянной.

Пусть , где – постоянная, т.к. значения этой функции при всех одинаковы, то ее приращение равно нулю и, следовательно,

Итак, производная постоянной равна нулю, т.е. .

б) Производная функции .

Составим приращение функции:

При нахождении производной использовали свойство предела произведения функций, первый замечательный предел и непрерывность функции .

Таким образом, .

Связь между дифференцируемостью функции и ее непрерывностью

Функция, имеющая производную в точке , называется дифференцируемой в этой точке. Функция, имеющая производную во всех точках некоторого промежутка, называется дифференцируемой на этом промежутке.

Теорема. Если функция дифференцируема в точке , то она непрерывна в этой точке.

Доказательство. Придадим аргументу произвольное приращение . Тогда функция получит приращение . Запишем равенство и перейдем к пределу в левой и правой частях при :

Поскольку у непрерывной функции бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то теорему можно считать доказанной.

Замечание. Обратное утверждение не имеет места, т.е. из непрерывности функции в точке, вообще говоря, не следует дифференцируемость в этой точке. Например, функция непрерывна при всех , но она не дифференцируема в точке . Действительно:

Предел бесконечен, значит, функция не дифференцируема в точке .

Таблица производных элементарных функций

Замечание. Напомним свойства степеней и корней, используемые при дифференцировании функций:

Приведем примеры нахождения производных.

1) .

Производная сложной функции

Пусть . Тогда функция будет сложной функцией от x .

Если функция дифференцируема в точке x , а функция дифференцируема в точке u , то тоже дифференцируема в точке x , причем

Полагаем , тогда . Следовательно

При достаточном навыке промежуточную переменную u не пишут, вводя ее лишь мысленно.

Дифференциал

К графику непрерывной функции в точке проведем касательную MT , обозначив через j ее угол наклона к положительному направлению оси Ох. Так как , то из треугольника MEF следует, что

Введем обозначение

Это выражение называется дифференциалом функции . Итак

Замечая, что , т.е. что дифференциал независимой переменной равен ее приращению, получим

Таким образом, дифференциал функции равен произведению ее производной на дифференциал (или приращение) независимой переменной.

Из последней формулы следует, что , т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.

Дифференциал функции dy геометрически представляет собой приращение ординаты касательной, соответствующее приращению аргумента Dх .

Из рисунка видно, что при достаточно малом Dх по абсолютной величине можно взять приращение функции приближенно равным ее дифференциалу, т.е.

Рассмотрим сложную функцию , где , причем дифференцируема по u , а – по х . По правилу дифференцирования сложной функции

Умножим это равенство на dx :

Так как (по определению дифференциала), то

Таким образом, дифференциал сложной функции имеет тот же вид, если бы переменная u была не промежуточным аргументом, а независимой переменной.

Это свойство дифференциала называется инвариантностью (неизменяемостью) формы дифференциала .

Пример. .

Все правила дифференцирования можно записать для дифференциалов.

Пусть – дифференцируемы в точке х . Тогда

Докажем второе правило.

Производная неявной функции

Пусть дано уравнение вида , связывающее переменные и . Если нельзя явно выразить через , (разрешить относительно ) то такая функция называется неявно заданной . Чтобы найти производную от такой функции, нужно обе части уравнения продифференцировать по , считая функцией от . Из полученного нового уравнения найти .

Пример. .

Дифференцируем обе части уравнения по , помня, что есть функция от

Лекция 4. Производная и дифференциал функции одной переменной

Определение: Производной от функции в точкеназывается предел, к которому стремится отношение ее приращенияв этой точке к соответствующему приращениюаргумента, когда последнее стремится к нулю:

Т.е., если определена в, то

Теорема 1:

График функции имеет невертикальную касательную тогда и только тогда, когда существует конечное значение производной этой функции в данной точке.

Доказательство:

Пусть существует значение f’()-конечное, тогда

Пусть существует невертикальная касательная => существует - конечный.

Секущая стремится к касательной.

Теорема доказана.

Билет 2 Непрерывность функции, имеющей производную.

Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если

Теорема: (необходимое условие существования производной)

Если функция имеет конечнуюв точке, тонепрерывна в точке.

Доказательство:

Следовательно - непрерывна в точке.

Теорема доказана.

Замечание : обратное утверждение неверно, если функция непрерывна в точке, то отсюда не следует, что она имеет производную в этой точке.

Утверждение : если функция имеет в точке правую и левую производную, то она непрерывна и справа и слева.

Билет 3

Производная суммы, произведения, частного.

Производная обратной функции.

Определение дифференцируемой функции. Необходимое и достаточное условие дифференцируемости.

Пусть функция имеет производную в точке(конечную):.

Тогда для достаточно малыхможно записать в виде суммыи некоторой функции, которую мы обозначим через, которая стремится к нулю вместе с:,

и приращение в точке может быть записано в виде:

или (1) ,

ведь выражение понимается как функция оттакая, что ее отношение кстремится к нулю вместе с.

Пояснение:

Определение .

Функция называется дифференцируемой в точке, если ее приращение можно представить в виде:(2),

где А не зависит от , но вообще зависит от.

Теорема 1:

Для того, чтобы функция была дифференцируемой в точке, необходимо и достаточно, чтобы она имела конечную производную в этой точке.

Доказательство:

Достаточность условия доказана выше: из существования конечной производной следовала возможность представленияв виде (1), где можно положить.

Необходимость условия . Пусть функция дифференцируема в точке. Тогда из (2), предполагая, получаем.

Предел правой части при существует и равен А:.

Это означает, что существует производная . Теорема доказана.

Билет 6 Дифференциал функции, его геометрический смысл.

Если функция f имеет производную f΄(x o ) в точке x o , то существует предел , где Δf=f(x o + Δx)-f(x o ) ,,или, гдеA=f΄(x o ) .

Определение:

Функция f дифференциируема в точке x o , если ее приращение представимо в виде:

Где A Δx=df . (*)

Дифференциал - это главная линейная часть приращения функции.

Если существует конечная производная f΄(x o ) в точке x o , то функция f(x) дифференцируема в этой точке.

Верно и обратное: если функция f дифференцируема в точке x o , т.е. ее приращение представимо в виде (*), то она имеет производную в точке x o , равную A :

Геометрический смысл дифференциала:

A и B – точки графика f(x) , соответствующие значениям x o и (x o + Δx) независимой переменной. Ординаты точек A и B соответственно равны f(x o ) и f(x o + Δx) . Приращение функции Δf=f(x o + Δx)-f(x o ) в точке x o равно длине отрезка BD и представимо в виде суммы Δf=BD=DC+CB , где DC=tgα Δx=f΄(x o ) Δx и α есть угол между касательной в точке A к графику и положительным направлением оси x . Отсюда видно, что DC есть дифференциал функции f в точке x o :

DC=df=f΄(x o ) Δx .

При этом на долю второго члена CB приращения Δf приходится величина . Эта величина, при больших Δx , может быть даже больше, чем главный член, но она есть бесконечно малая более высокого порядка, чем Δx , когда Δx→0 .

Теорема: Если функция y = f (x ) дифференцируема в некоторой точке x = x 0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x 0 функция y = f (x ) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x | непрерывна для всех x (–Ґ< х < Ґ), но в точке x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

Производная сложной функции

Теорема: Пусть функция , определенная и непрерывная в окрестности , имеет производную в точке . Функция определена и непрерывна в окрестности , где , и имеет производную в точке . Тогда сложная функция имеет производную в точке и

где и - б.м.ф. Тогда

и , где б.м.ф. в точке .

28. Производная суммы, произведения и частного двух функций.

Производная суммы (разности) функций

Производная алгебраической суммы функций выражается следующей теоремой.

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная произведения двух функций не равана произведению производных этих функций.

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0 , то производная частного этих функций вычисляется по формуле

29. Производная обратной функции. Производная функции, заданной параметрически.

ТЕОРЕМА (производная обратной функции)

Пусть непрерывная, строго монотонная (возрастающая или убывающая) функция на отрезке и имеющая в точке производную . Тогда обратная функция имеет производную в точке и

ДОК.

= .

Теорема. (производная функции, заданной параметрически) Пусть функция x = φ(t) имеет обратную функцию t = Ф(x). Если функцииx=φ(t) , y = ψ(t) дифференцируемы и φ"(t) ≠ 0 , тогда

Доказательство

Так как функция x = φ(t) имеет обратную функцию, то формально y можно выразить черезx : y = ψ(Ф (x)) . Так как функция x = φ(t) дифференцируема, то, по теореме 5 , функция t = Ф(x) также дифференцируема.

Используя правила дифференцирования, получаем чтд

Аналогичную формулу можно получить и для второй производной y"" x :

Окончательно получаем

30. Производные высших порядков. Формула Лейбница.

Если f определена на интервале (a,b)®R, диф-ма в " точке xÎ(a,b) то на (a,b) возникает новая функция f’ :(a,b)®R, значение которой в точке x=f’ (x). Функция f’ сама может иметь производную (f’ )’ : на (a,b)®R она по отношению к исходной функции называется второй производной от f и обозначается f” (x), d 2 f(x)/dx 2 или f” xx (x), f” x 2 (x); Опр . Если определена производная f (n -1) (x) порядка n-1 от f то производная порядка n определяется формулой f (n) (x)=(f n -1))’(x). Для нее принято обозначение f (n) (x)=d n f(x)/dx n – ф-ла Лейбница , f (0) (x):=f(x).

31. Понятие дифференцируемости функции и первого дифференциала. Необходимое и достаточное условие дифференцируемости.

1.Дифференциалом функции y = f(x) называется главная линейная относительно D x часть приращения D y, равная произведению производной на приращение независимой переменной

dy = f" (x )D x.

Заметим, что дифференциал независимой переменной равен приращению этой переменной dx = D x. Поэтому формулу для дифференциала принято записывать в следующем виде:

dy = f" (x )dx.

2. Дифференцируемость. Функция называется дифференцируемой в точке x, если ее приращение ∆y в этой точке может быть представлено в виде: ∆y=A∆x + α(∆x) ∆x, где A не зависит от ∆x, α и α(∆x) – бесконечно малая функция относительно ∆x при ∆x→0.

32. Геометрический смысл производной и дифференциала. Касательная и нормаль к графику.

Пусть f определена на (a,b) и непрерывна в точке x 0 Î(a,b), пусть y 0 =f(x 0), M 0 (x 0 ,y 0); x 0 +DxÎ(a,b), Dy=f(x 0 +Dx)-f(x 0), M(x 0 +Dx, y 0 +Dy). M 0 M: y=k(x-x 0)+y 0 (1),

1 )Если $ кон. предел lim D x ® 0 k(Dx)=k 0 то прямая y=k 0 (x-x 0)+y 0 (2) назыв.

(наклонной) касательной к графику f в точке (x 0 ,y 0);

2 ) Если $ бесконечный предел

lim D x ® 0 k(Dx)=¥, то прямая x=x 0 – вертикальная касательная к графику в точке (х 0 ,у 0);

При х=х 0 (2) – предельное положение (1) т.о. предельное положение секущей М 0 М

Dх®0 это касательная y=f(x) в точке х 0 , т.к. lim D x ® 0 k(Dx)=lim D x ® 0 Dy/Dx=f’ (x 0) то уравнение

касательной имеет вид y=f’ (x 0)(x-x 0)+ y 0 , где y 0 =f(x 0) (3). Из 3 получаем что производная в точке х 0 =tga, a - угол между касательной и осью Ох, первое слагаемое f’ (x 0)(x-x 0)=f’ (x 0)Dx, Dx=x-x 0 является диф-ом dy в точке х 0 Þ y-y 0 =dy т.о. дифференциал функции равен приращению ординаты касательной в соответствующей точке графика.

3 )Если lim D x ® 0 Dy/Dx=¥, то касательной является прямая х=х 0 при этом в точке х 0 бескон. производная может существовать или не существовать.

33. Инвариантность формы первого дифференциала. Дифференциалы высших порядков, неинвариантность их формы в общем случае .

Дифференциалы высших порядков . Диф-ал от диф-ла первого порядка dy=f’(x)dx функции y=f(x) (рассматриваемого только как ф-и переменной х т.е. приращение аргумента х (dx) принимается постоянным, при условии что повторное приращ-е переменной х совпадает с начальным) называется вторым диф-ом d 2 f(x):d(df(x))=d(f’(x)dx)=d(f’(x))dx=f”(x)dxdx=f”(x)dx 2 отсюда f”(x)=d 2 f(x)/dx 2 ; Опр . Диф-ом n-го порядка n=1,2… называется дифференциалом от дифференциала порядка n-1 при условии что в диф-ле берутся одни и те же приращения dx, независимого от х. d n f(x)=d(d n -1 f(x)) не трудно видеть, что d n f(x)=f (n) (x)dx n (dx n =(dx) n) Þ f (n) (x)=d n f(x)/dx n .

Неинвариантность формы дифференциала порядка выше первого

Рассмотрим случай, когда х является не независимой переменной, а функцией от другой переменной

Теперь в правой части формулы (3) от переменной u зависит не только функция f (x ), но и дифференциал dx . Следовательно

Сравнивая формулы (2) и (4), убеждаемся, что дифференциалы второго (и более высоких порядков) не обладают инвариантностью формы.

34. Экстремумы функции. Необходимые условия экстремума (теорема Ферма).

Точки экстремума

Экстре́мум - максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума . Соответственно, если достигается минимум - точка экстремума называется точкой минимума , а если максимум - точкой максимума . В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум) .

Точка x 0 называется точкой строгого локального максимума (минимума) функции f (x ), если для всех значений аргумента из некоторой достаточно малой δ - окрестности точки х 0 выполняется неравенство

f (x ) < f (x 0) (f (x ) > f (x 0))

при х ≠ x 0 .
Локальный максимум и локальный минимум объединяются общим названием экстремум. Из определения следует, что понятие экстремума носит локальный характер в том смысле, что неравенство f (x ) < f (x 0) (f (x ) > f (x 0)) может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки x 0 .

Функция y=f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом, из дифференцируемости функции следует ее непрерывность.

Доказательство . Если, то

где б бесконечно малая величина, т.е. величина, стремящаяся к нулю при Дx>0. Но тогда

Дy=f "(x 0) Дx+бДx=> Дy>0 при Дx>0, т.е f(x) - f(x 0)>0 при x>x 0 ,

а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

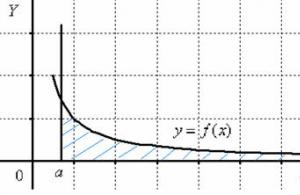
Рассмотрим на рисунке точки а, b, c.

В точке a при Дx>0 отношение не имеет предела (т.к. односторонние пределы различны при Дx>0-0 и Дx>0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Дx>0 отношение является знакопостоянной бесконечно большой величиной. Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки - "точка перегиба" c вертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип - "точка возврата" с вертикальной касательной - частный случай угловой точки.

1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке

Покажем, что она не имеет производной в этой точке.

f(0+Дx) = f(Дx) = |Дx|. Следовательно, Дy = f(Дx) - f(0) = |Дx|

Но тогда при Дx< 0 (т.е. при Дx стремящемся к 0 слева)

А при Дx > 0

Т.о., отношение при Дx> 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная "кривая" не имеет определенной касательной (в этой точке их две).

2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x= 0.

Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.